The investigation of the growth prediction of the COVID-19 pandemic was carried out in three countries with a similar number of habitants, namely Austria, Switzerland, and Israel. To this aim, we compare the results obtained with Gompertz’s growth model and the Box–Jenkins ARIMA statistical model. All three countries took similar lockdown measures, border closures, restriction of movement, and closure of shops; the most restrictive were Israel and Austria, while Switzerland’s rules were the least restrictive for its citizens. All three countries are now beginning the easing of lockdown of its citizens and the opening of trade. Relaxed confinement measures were first made in Austria, starting April 14, then Israel on April 16, and, finally, Switzerland on April 27. The measures taken have been effective differently in each country, as can be seen in Table 1A.36–39
 | Table 1 Summary of Infected and Mortality Data by Country. |
These data evidence that the most efficient systems for isolation/lockdown, at the moment, were implemented by Austria and Israel, with an infection rate of 1,855 and 1,937 people per million inhabitants, respectively. In contrast, Switzerland reached an infection rate nearly twice that of Austria and Israel, with 2,560 cases per million inhabitants. Regarding deaths, it can be seen that the highest mortality rate was in Switzerland, where they had a death rate of more than 6.2% of those infected, and a per capita mortality of 220 deaths per million inhabitants. The country with the lowest mortality rate is Israel, with a 1.7% mortality rate and 32 deaths per million inhabitants.
In this paper, we report on a study of the increase in numbers of infected and dead due to COVID-19 using the Gompertz growth model and the ARIMA statistical model. Specifically, to obtain the growth forecasts we employed the following procedure (summarized in Figure 1):
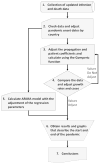 | Figure 1 Overview of the Research Flowchart. |
-
Collection of data on infected people detected by tests and deaths from each country of the investigation until May 19, 2020.
-
Verification of the data and adjustment of the initial pandemic and death rates per country to make the calculations.
-
Adjustment of the assumed values of the growth, spread rate, and the maximum number of predicted cases of infection and death by country; calculation of the number of infected and dead individuals in each country using the Gompertz growth function.
-
Comparison between the calculated and the real data, adjusting the growth coefficients and the forecast of the cases, to get the values that best fit the actual situation; verification of the validity of the data collected by calculating the R2, root mean squared error (RMSE), and mean absolute percentage error (MAPE) values for each estimate and country.
-
Performance of the statistical calculations of the ARIMA model with adjustment of the regression parameters; verification of the validity of the data obtained by calculating the R2, RMSE, and MAPE values for each estimate and country.
-
Construction of a sigmoid graph describing the growth in number of infected and dead, and the estimated end of the pandemic for each country; to this aim, we used the predicted values that best fit the reality of each country.
-
Concluding description of more precise methods to contain future pandemics.
ARIMA Method
The ARIMA method attempts to forecast the values of a variable by using only past observations. To extract the observed patterns, the structural conditions that make up the series, such that it remains constant, should be satisfied. This is known after its creators as the Box–Jenkins model.
40,41 It is widely used for the analysis of economic series, as well as in hydrology or medicine.
42,43 However, the field in which the ARIMA methodology finds its central role for prediction purposes is with short-term prediction and in series with a seasonal component.
44 The ARIMA model provides a general methodology for the analysis of a single variable in the series that shows a clear dependence between the present and past values.
The generic name ARIMA derives from its three components: autoregressive (AR), integrated (I), and moving averages (MA). The ARIMA model presents an explicit equation that allows us to describe an observation of the series as a linear function of previous data and errors due to chance. Moreover, it can include a cyclical or seasonal component that describes each of the elements that can be part of the model, as well as the notation generally used to describe them, which is used in this study. The general function45,46 represented by the ARIMA model (p, d, q) is defined as follows:
∅(β) (1-β)dXt=c+θ(β)ɛt | (Eq. 1) |
where Xt is the variable to study, c is a constant, and ɛt is the error or residue term, which follows a normal distribution of zero mean and constant variance. The term (1-β)d is applied to the original series to make it stationary, and d corresponds to the order of part I of the ARIMA model. Ø(β) and θ(β) are polynomials of order p and q that depend on the delay operator β.
Gompertz Model
The other mathematical model that we have used to compare the growth forecasts of the pandemic is the Gompertz model, which belongs to the family of sigmoid curve modeling.
47 There are different types of Gompertz curves depending on the parameters that compose them, but they all have a double exponential as a common characteristic element. With this function defined for human mortality, Charles P. Winsor
48 began to study the growth of biological phenomena. He proposed the Gompertz model, which was later used by many authors in growth studies of all kinds.
49–51 There is a multitude of options when it comes to expressing the Gompertz curve model because this name was assigned to a wide variety of curves, which have in common being double exponential. We use the following model to assess the growth and development of COVID-19:
f(t)=k{(ln(X0k)) (e-α(t-t0))},t≥t0, α>0, k>X0>0 | (Eq. 2) |
Considering k the maximum predicted number of patients infected or dead in the development of the pandemic, X0 is the number of initial patients, infected or dead, when the epidemic starts at time t0. We also consider t the prediction time, and α is the growth rate characteristic of the pandemic. For biological growth calculations, we restrict the values of t (t≥t0≥0) and the initial number of patients X0=f(t0)>0.
This sigmoid curve is limited in time, shows a monotonous increase, and presents an inflection point. The curve changes from concave to convex at this point, reaching approximately 37% of the growth. The inflection point depends on X0 and can be defined for k>X0:
Inflection point dimension (IPD):
IPD=(lnkX0b+t0,ke) | (Eq. 3) |
and the approximate percentage of growth at that point (APG):
APG=37×(1-X0k-X0)% | (Eq. 4) |
Data on confirmed cases and deaths were obtained from the WHO,37 with daily reports submitted worldwide from the European Center for Disease Prevention and Control (ECDC).39 We consider the data of infected individuals from February 25, 2020, for all three countries. On the other hand, the day of the first death from COVID-19 was different for each country, namely March 5 for Switzerland, March 12 for Austria, and March 21 for Israel. The cumulative curves of deaths and infections for the study countries are illustrated in Figure 2.
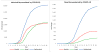 | Figure 2 COVID-19 Data from Infected (left) and Dead (right). |
We performed the forecast calculations for the Gompertz model and the ARIMA model with the data obtained of the numbers of infected and dead. Based on the mathematical modeling software IBM SPSS Statistics,52 we verified and calculated multiple possibilities for the Gompertz model for the growth rate α of deaths and infections, and with various values of the k parameter with the maximum expected number of infected and dead by country. Moreover, we took into account the different possibilities of the indicators (p, d, q) of the ARIMA model to obtain the values closest to the real data collected up to the date of the study (May 19, 2020). Based on the different results, we compared the predicted values with the actual values. To this aim, we worked out a quantitative examination of the fit using error measurement indices, commonly used to evaluate prediction models.53 We used Karl Pearson’s R2 regression index54 to justify its greater or lesser correlation.55 Additionally, we compared the model accuracy of the different regressions according to the RMSE56 and MAPE,57 which are forecast indicators that measure the size of the absolute error in percentage terms, giving us a relative measure of the error. The functions used for accuracy calculations are as follows:
RMSE=⌊1t∑i=1t(up-uo)2⌋1/2 | (Eq. 5) |
MAPE=100t∑i=1t|kr-kfkr| | (Eq. 6) |
where t denotes the number of observations, u is the residue of the estimates, the subscript p refers to the predicted residue whereas subscript o is the observed residue, kr is the actual number of infected or dead, and kf is the estimated number of infected or dead according to the analyzed prediction model.
